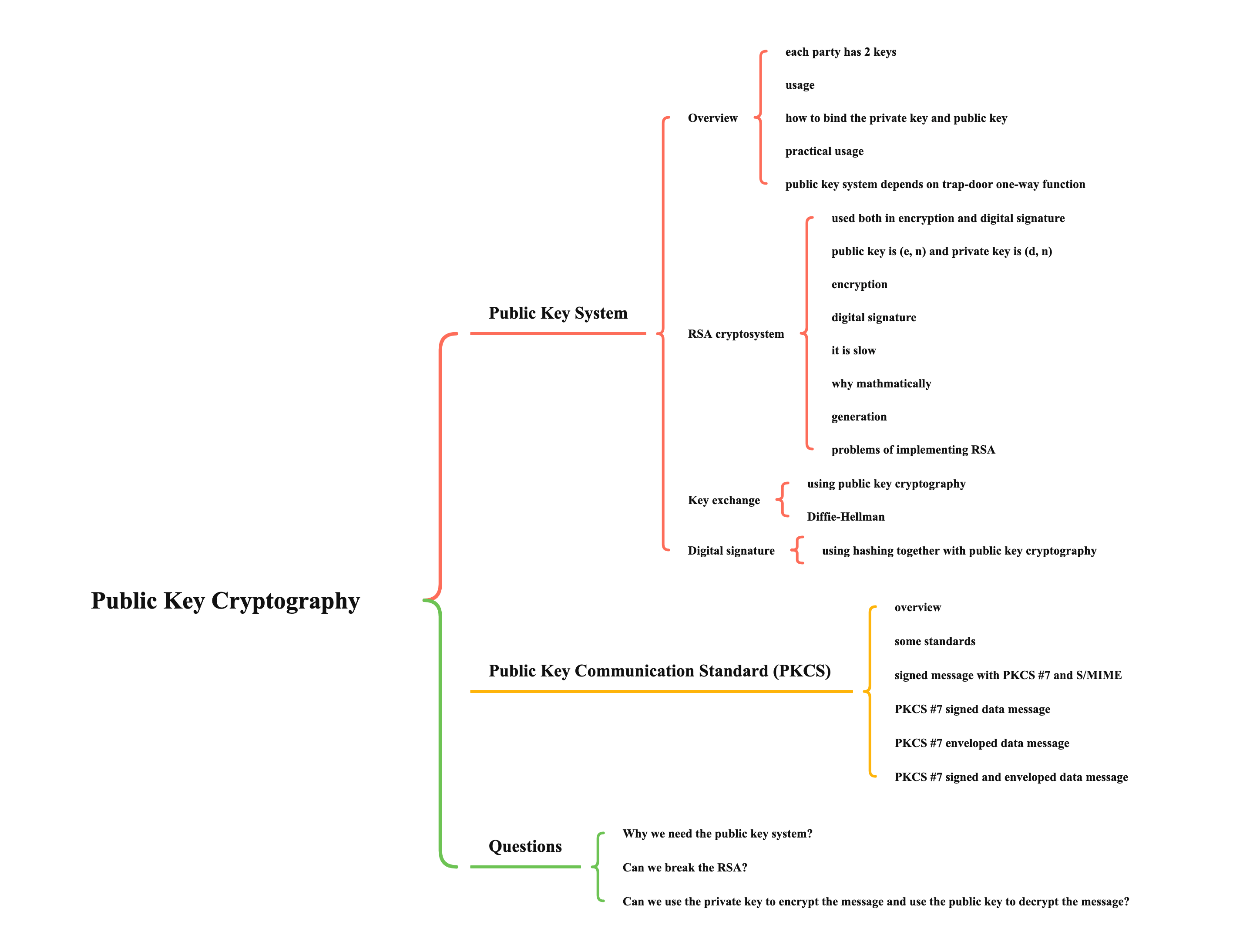
Public Key System

Overview

  • each party has 2 keys (no key distribution)
    • public key (open to the public)
    • private key (secret to the owner)
      • mathematically, it is difficult to find the private key according to the public key
      • security strength depends on key length
  • usage
    • encryption
    • digital signature (unforgeable, no encryption -> message is public)
      • verfiy the origin of a message (not tampered)
      • verify the identity of the sender (non-repudiation)
      • reslove any authentication issues between the sender and the receiver
  • how to bind the private key and public key
    • using public key infrastructure
  • practical usage
    • encryption and signature can be used together
    • combined with hash functions and symmetric key system
  • public key system depends on trap-door one-way function
    • examples
      • exponentiation: \(b = a^e\ mod\ p\)
      • factorization: \(n = p\times q\)
        • RSA use this, except bitcoin (ECC)
        • multiplication & factorization
          • e.g. \(47\times 59=2773\), but if you just got the 2773, how to find prime factors

RSA cryptosystem

  • used both in encryption and digital signature
  • public key is (e, n) and private key is (d, n)
  • encryption
    • encrypt a message m (< n)
      • compute \(c=m^e\ mod\ n\)
    • decrypt a ciphertext c (< n)
      • compute \(m=c^d\ mod\ n\)
  • digital signature
    • sign a message m (< n)
      • compute \(s=m^d\ mod\ n\)
    • verify the signature s of a message m (< n)
      • compute \(m1=s^e\ mod\ n\)
      • check if m1 == m?
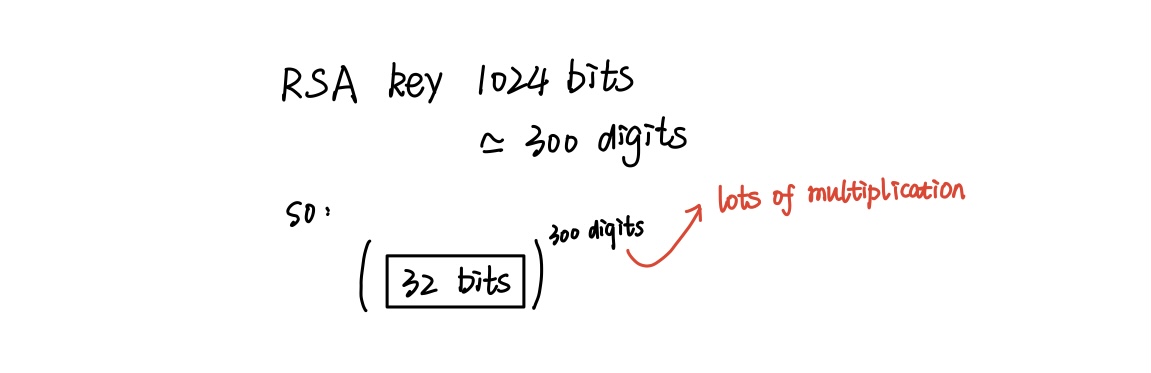
  • it is slow
    • because of too much exponentiation & multiplication
    • underlying methods are symmetric key (encryption) and hashing (digital signature)
    • example
  • why \(M=M^{ed}\ mod\ n\)
    • fermat's theorem
      • \(m^{p-1}\ mod\ p=1\)
    • euler's generalization
      • \(m^{(p-1)(q-1)}\ mod\ n=1\) (\(n=p\times q\))
      • -> \(m^{(p-1)\times(q-1)}\times m\ mod\ n=1\times m\)
      • -> \(m^{(p-1)\times(q-1)+1}\ mod\ n=m\)
      • -> \(e\times d=(p-1)\times(q-1)+1\)
      • specific condition
        • if \(e\times d=41\), how to find e and d
          • use modulus with n=40, i.e.
            • \(e\times d=41\ mod\ 40\)
            • \(e\times d=1\ mod\ 40\)
            • set e = 3
            • \(3\times d=1\ mod\ 40\)
            • use extended euclidean algorithm, we find d=27
            • \(3\times 27=81=1\ mod\ 40\)
  • generation
    • generate 2 large primes p, q
    • compute n (the modulus) = \(p\times q\)
    • compute \(\psi(n)=(p-1)\times (q-1)\)
    • generate e relatively prime to \((p-1)\times (q-1)\), i.e. gcd(\(\psi(n)\), e) = 1
    • compute inverse of e: \(d=e^{-1}\ mod\ ((p-1)\times(q-1))\)
    • public key is (e, n) and private key is (d, n)
    • 1024-bit RSA means n has 1024 bits
  • problems of implementing RSA
    • both encryption and decryption use exponentiation
      • use Square & Multiply Exponentiation -> faster
    • in key generation, we need to compute inverse of e
      • use extended Euclid's Algorithm -> more efficient
    • in key generation, we need to generate 2 large primes p and q
      • use probabilistic algorithm -> efficient to generate large prime number

Key exchange

  • using public key cryptography
    • A generate secret key (sk) randomly
    • A uses B's public key to encrypt sk and sends the encrypted key to B
    • B decrypted the encrypted sk using his private key
    • both A and B has the secret key and data can then be encrypted using any block ciphers with sk
    • but the secret key is generated by A, B has no control on the secret key
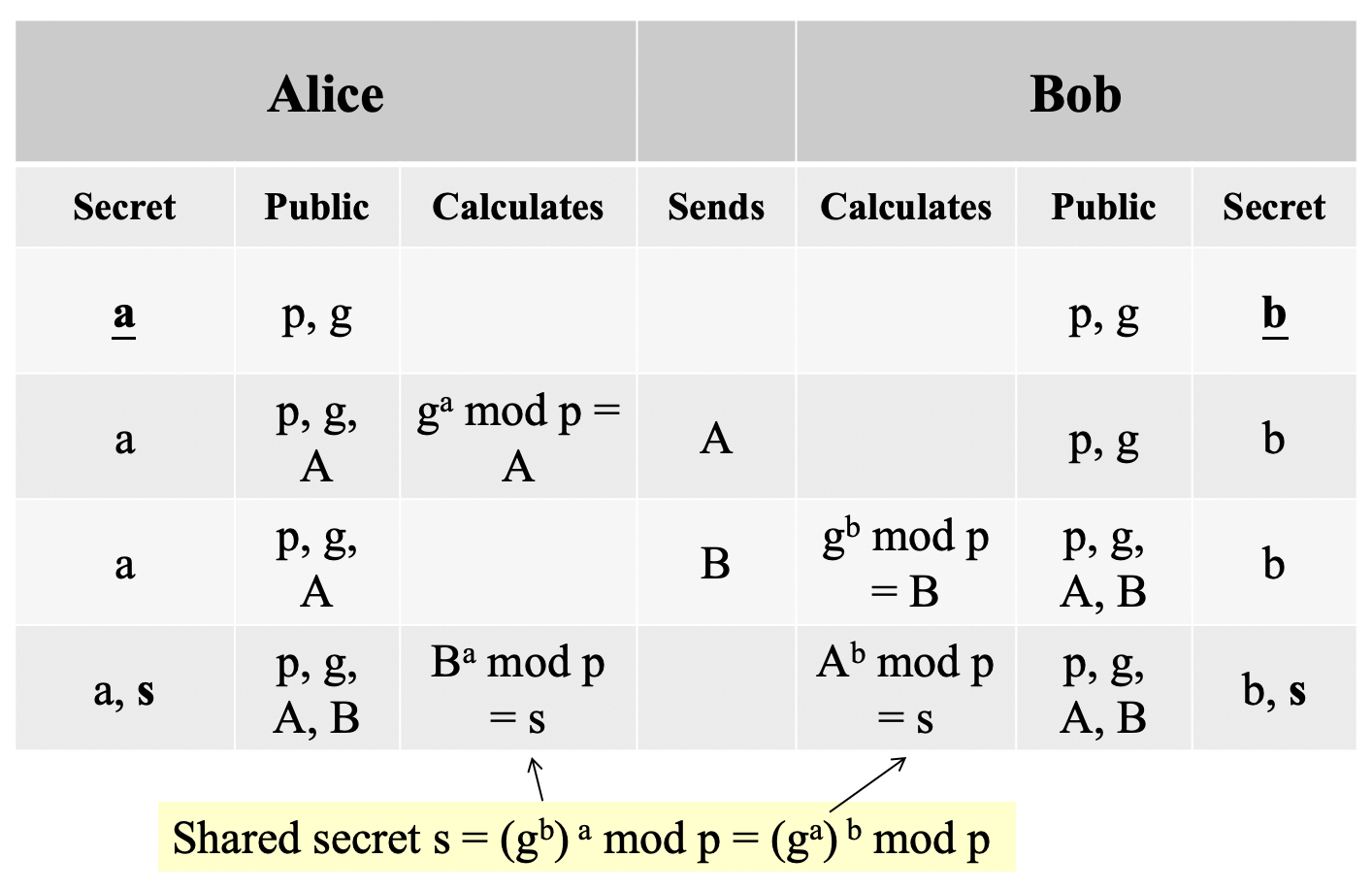
  • Diffie-Hellman

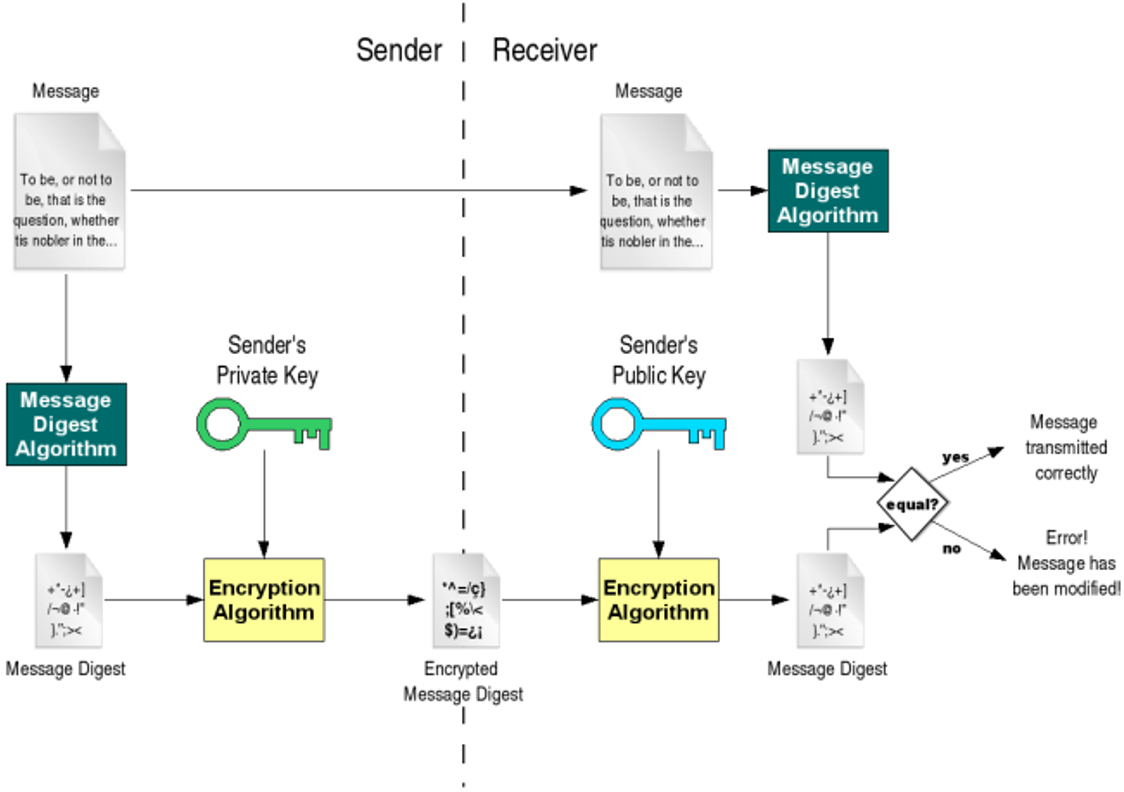
Digital signature

  • using hashing together with public key cryptography

Public Key Communication Standard (PKCS)

  • overview
    • group of public key cryptography standards, published by RSA lab (not a international standard, a industry standard)
    • include both algorithm-specific and algorithm-independent implementation standards
    • define an algorithm-independent syntax for digital signatures, digital envelopes (for encryption) and extended certificates
    • two algorithms (RSA and Diffle-Hellman key exchange) are specified in details
    • enable cryptographic algorithm implementers to conform to a standard syntax and achieve interoperability
  • some standards
    • PKCS #1: RSA cryptography standard
      • fundamental building block for all public key cryptography
      • defines a method for encrypting data using RSA
      • includes RSA key generation, key syntax, the encryption and decryption processes, signature algorithms
    • PKCS #5: password-based cryptography standard
      • defines how a password and a random number (salt) are to be mixed to together to form a symmetric key
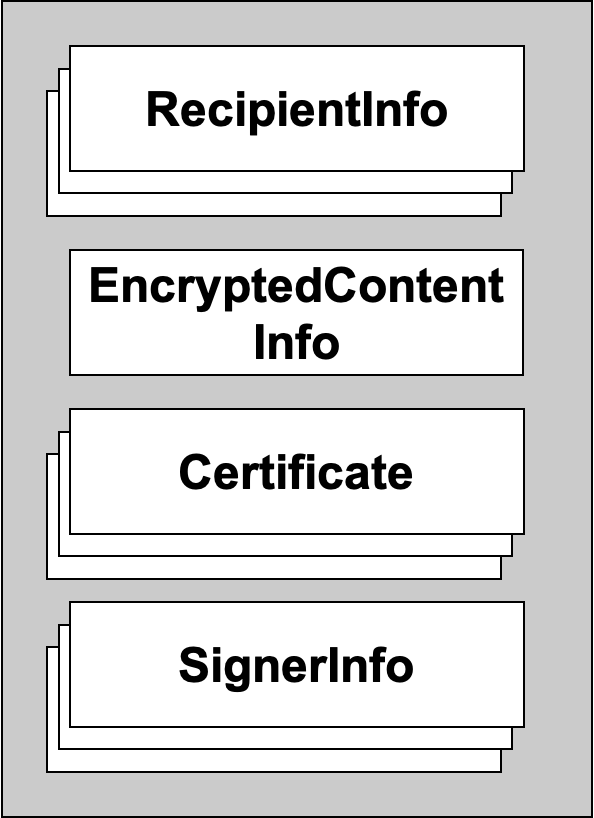
    • PKCS #7: cryptographic message syntax standard
      • specifies how to package information like signature algorithm, signer’s certificate, original message, signature bytes, … in a standard format
      • allows senders to encode the objects and receivers to decode the information in a predictable, interoperable way, using independent implementation
      • includes both signed data and enveloped data
    • PKCS #8: private-key information syntax standard
      • provides standard definitions for encoding and decoding private keys either in a raw form or in an encrypted format
    • PKCS #10: certification request syntax standard
    • PKCS #12: personal information exchange syntax standard
      • a transfer syntax for personal identity information, including private keys, certificates, …
  • signed message with PKCS #7 and S/MIME
    • MIME -> email
    • MD5 -> hash
    • RSA -> digital signature
    • email contains the algorithm, the message content, the signature as well as the public key
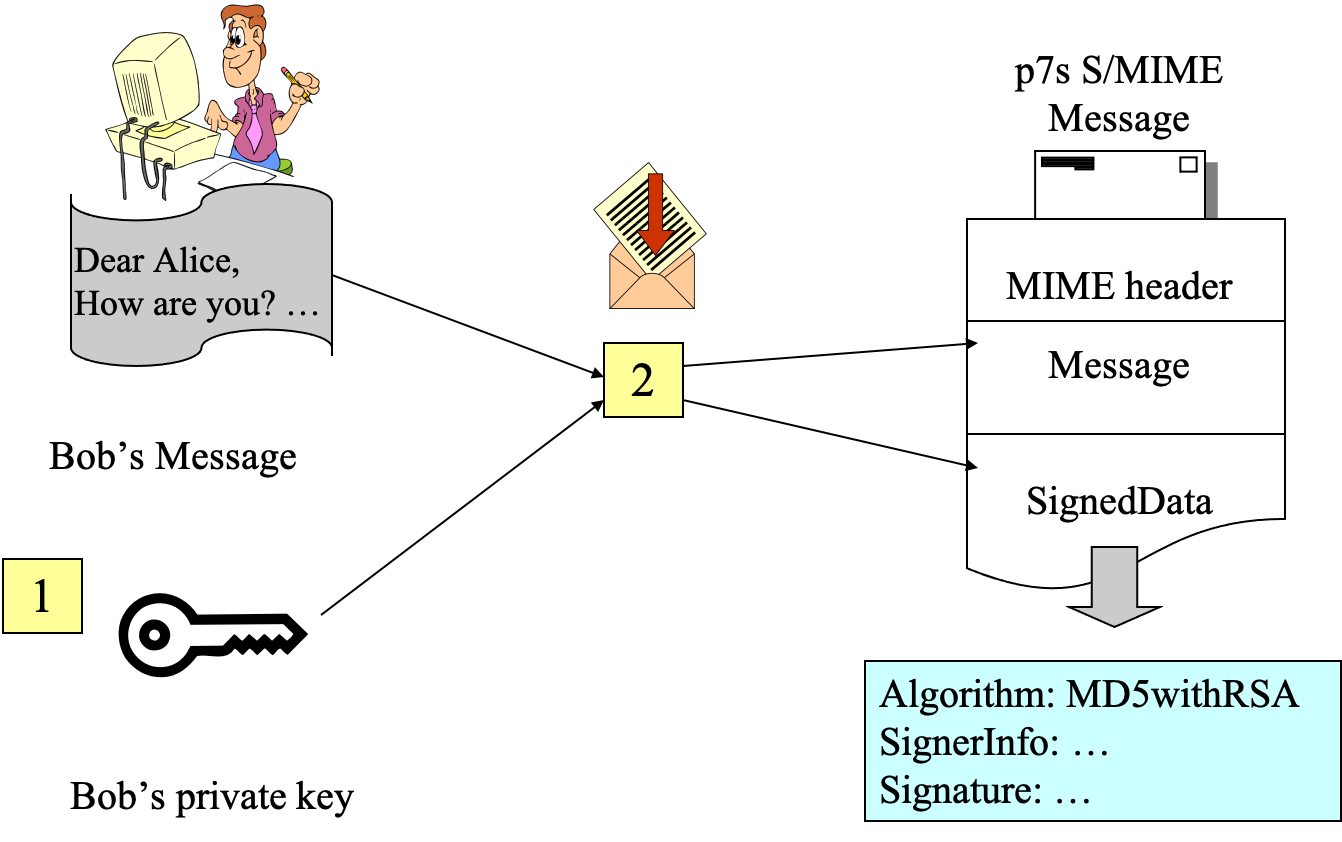
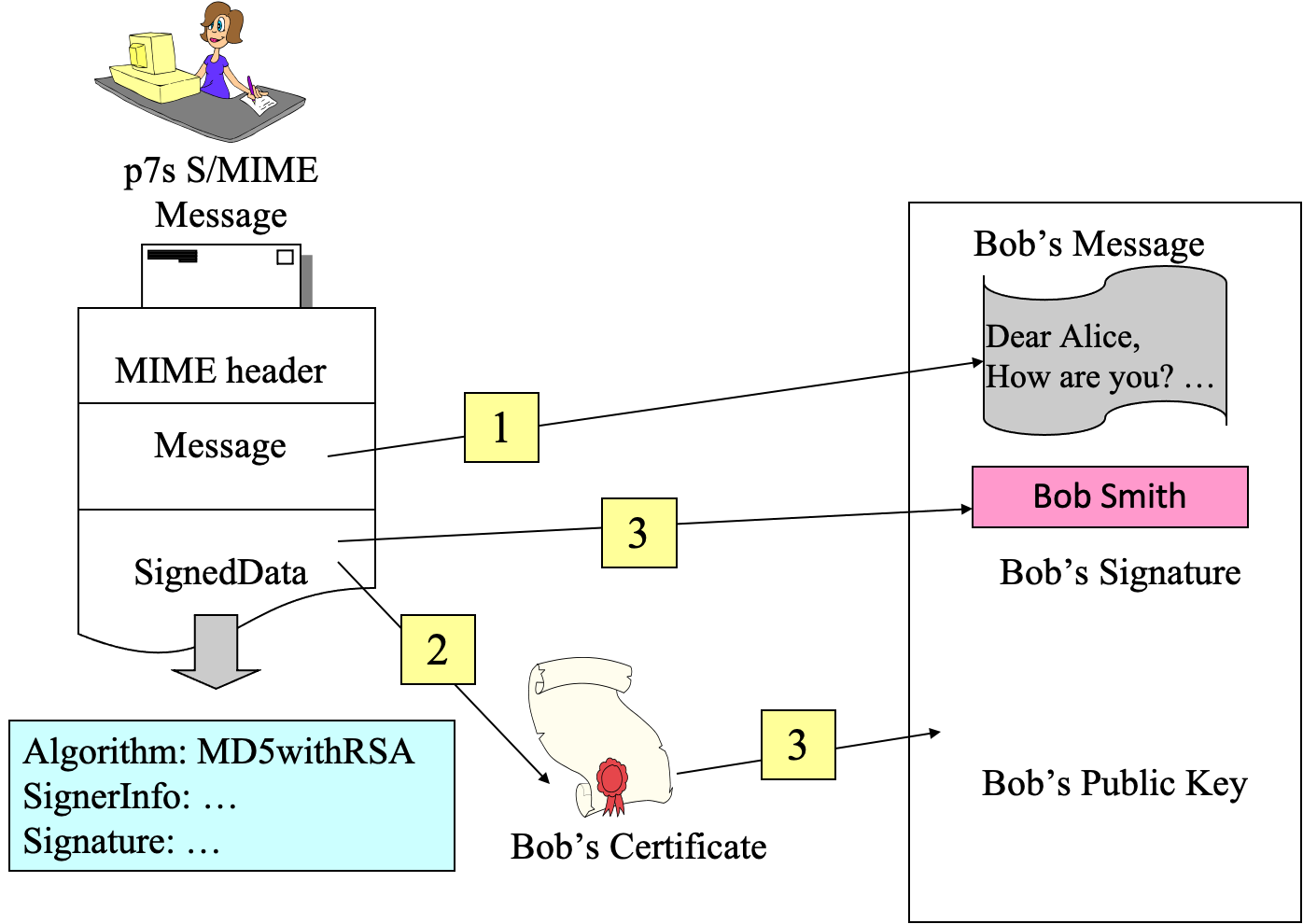
  • PKCS #7 signed data message
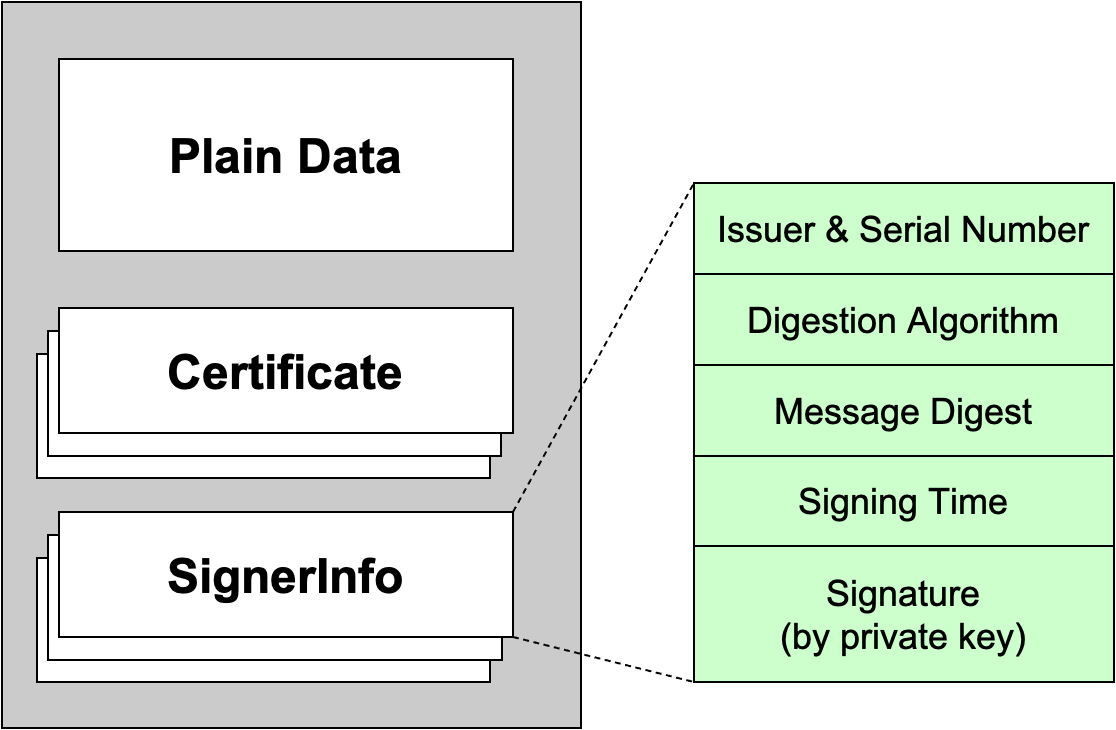
    • the same plaintext, generate different message digests (e.g., use SHA-256, MD5 at the same time), signing time, signature (e.g., RSA and other methods at the same time)
  • PKCS #7 enveloped data message
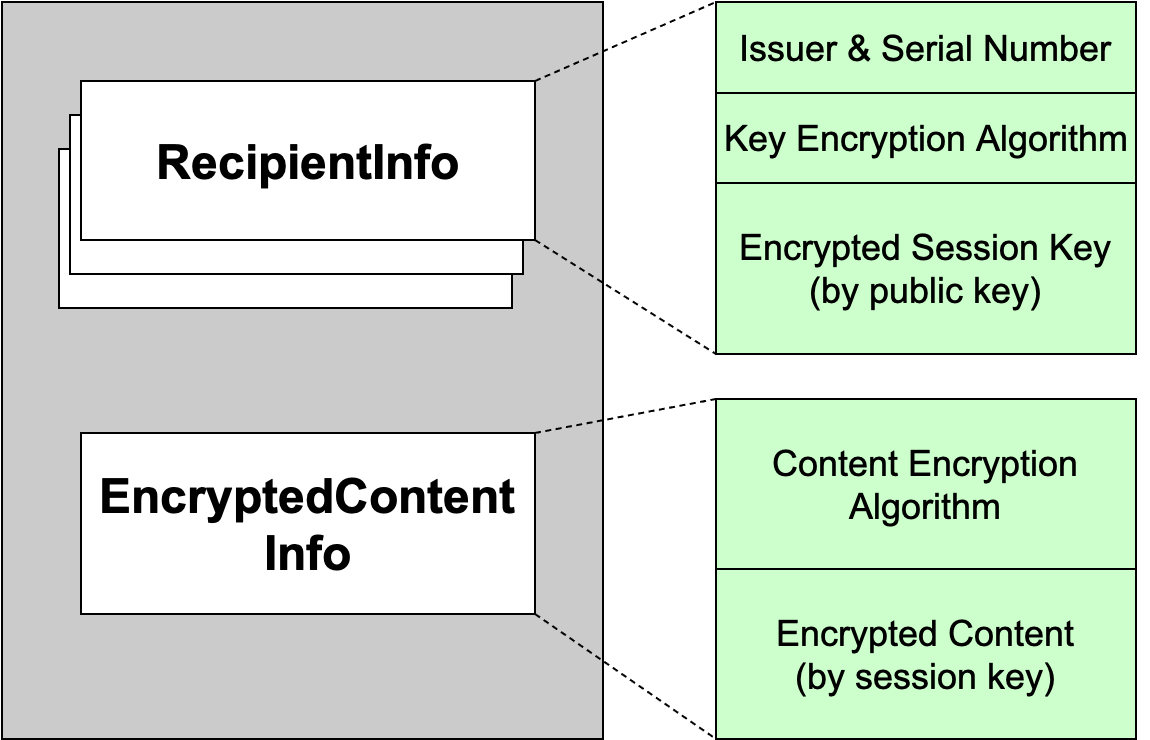
    • the same encrypted content, different recipient information (different people have different private keys and public keys)
  • PKCS #7 signed and enveloped data message

Questions

Q: Why we need the public key system?

A: Symmetric key system has the problem, which is key distribution.

Q: Can we break the RSA?

A: Because n is a large number generated by p and q, and this machinism use factorization, it is pretty difficult to break. To large extent, if you want to break, you need to try all the possiblities. Nowadays, we use may be 500 digits, so it is difficult to break. However, if you have the public key (e, n) and factor n, you can derive the private key.

Q: Can we use the private key to encrypt the message and use the public key to decrypt the message?

A: This process is digital signature, and the purpose is authentication and verification, not encryption and decryption.